Converting the Scout Index to the H3 Grid System

Abstract

Scaling geospatial indexing systems on a global level requires a framework that is standardized, consistent, and adaptable across formats. U.S. ZIP codes, while commonly used in U.S. applications such as the Scout Index, introduce limitations, including irregular sizes and shapes, boundary changes over time, and limited global applicability. This paper presents the conversion of the Scout Index from ZIP Code Tabulation Areas (ZCTAs) to the H3 hierarchical hexagonal grid system.

H3 provides a globally uniform and computationally efficient spatial reference that partitions the Earth into hexagons at 16 resolutions, each encoded as compact integer identifiers that support efficient storage, retrieval, and neighborhood operations. We explain how arbitrary polygons can be rasterized into H3 cells, enabling integration with external datasets such as global population density. We used this to design a sampling strategy of 3,000 locations across the U.S., E.U., U.K., and Australia. We further evaluate the impact of resolution choice on local business search rankings, finding that resolution 6 (hexagons with an edge length of ~3.2 km) captures statistically significant differences between rooftop and neighborhood-level searches while remaining geographically plausible for local users. Finally, we address challenges of representativeness in search behavior, noting that H3's spatial uniformity does not fully capture cultural or demographic variation, and propose refinements for future sampling.

By replacing ZIP codes with H3, the Scout Index gains a global, reproducible, and scalable foundation for analyzing search behavior across diverse geographies.

Introduction

Scaling geospatial indexing systems to a global level requires a standardized, consistent, and format-agnostic framework. U.S.A. ZIP codes, while useful for domestic applications, impose structural limits due to their irregular geometry, shifting boundaries, and lack of global analogues.

This paper outlines our conversion of the Scout Index from U.S.A. ZIP Code Tabulation Areas (ZCTAs) to the H3 hierarchical hexagonal grid system. H3's structure provides a globally uniform and computationally efficient foundation for analyzing location-based phenomena.

We detail the population-weighted sampling of 3,000 global locations and evaluation of H3 resolutions in modeling local search rankings. The results demonstrate that H3 resolution six balances spatial realism with computational efficiency, making it optimal for neighborhood-scale business analysis.

By replacing ZCTAs with H3, the Scout Index attains global scalability, reproducibility, and analytical precision in the study of local search behavior.

Key Highlights

• Standardization at Scale: H3 partitions the entire Earth into uniform hexagons across 16 resolutions, replacing the irregularity of ZIP codes with a consistent, global coordinate system.
• Efficiency and Hierarchy: Each cell is encoded as a unique 64-bit integer, enabling rapid lookups, aggregations, and neighborhood operations.
• Empirical Validation: Resolution 6 (~3.2 km edge length) captures statistically meaningful distinctions between rooftop and neighborhood search behaviors.
• Cross-Regional Sampling: A population-weighted approach selected 3,000 representative scan points across the U.S., E.U., U.K., and Australia, aligning global diversity with data integrity.

Why we made the change

Spatial data forms the backbone of search visibility analytics. Yet the geographic units we use, especially ZIP Codes, were never designed for this purpose. Originally designed for mail delivery, ZIP codes vary widely in area, shape, and population density.

While convenient, ZIP codes introduce severe analytical limitations. They are irregularly shaped, ranging from small urban blocks to massive rural expanses. This irregularity creates bias whenever they are treated as equivalent units of analysis. They are unstable because boundaries shift whenever the postal service changes routing, complicating longitudinal studies. Ultimately, they are confined to the United States, which limits their ability to conduct global analysis.

In applications such as the Scout Index, these weaknesses are amplified because the goal is to capture consistent patterns of search behavior at scale. A dense urban ZIP code may encompass only a few blocks, whereas a rural ZIP code may span multiple towns; therefore, treating them as equivalent can lead to distorted results

To move beyond these limits, we adopted H3, an open-source, hierarchical grid developed by Uber for geospatial indexing. Unlike administrative boundaries, H3 divides the planet into uniform hexagons, enabling computationally efficient, globally standardized spatial operations (Uber Technologies, 2018). This is also part of the reasoning for using H3 in our Scout Product.

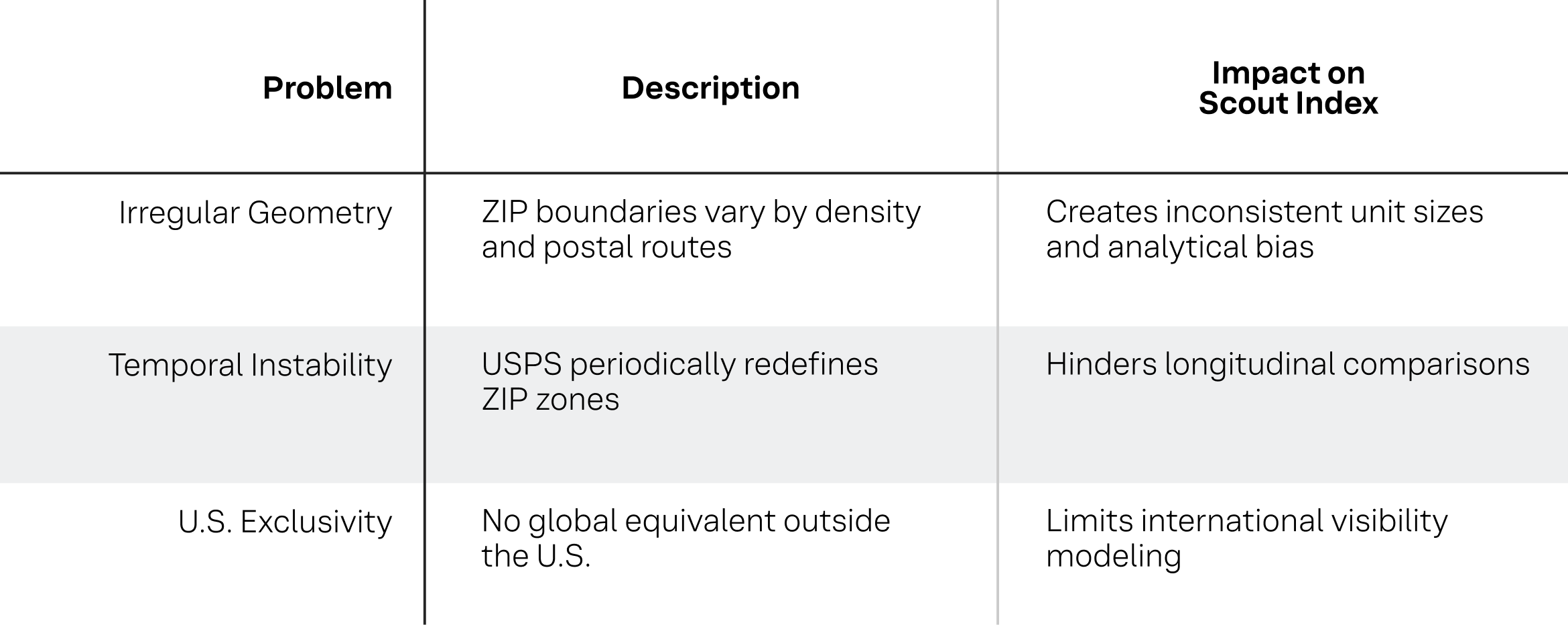
Table 1

The convenience of ZIP codes masks their analytical weaknesses. In a data ecosystem spanning continents, they represent an outdated construct that no longer aligns with the granularity or universality required by AI-driven systems.

The H3 indexing system allows us to seamlessly expand our analytics globally. Since July 2025, Yext has accumulated more than 65 million AI citations (and rapidly growing!) across leading Search Generative Experiences, giving us a large-scale view of how AI systems reference businesses in real search scenarios. Because we probe for your brand’s presence locally, the dataset captures how citations vary at a neighborhood level, aligning with what citations customers can expect to see at each of your locations across the globe. This creates a clear, data-rich foundation for understanding AI visibility across regions and categories, helping organizations see how they appear in AI answers today and track how that presence evolves as AI search continues to grow.

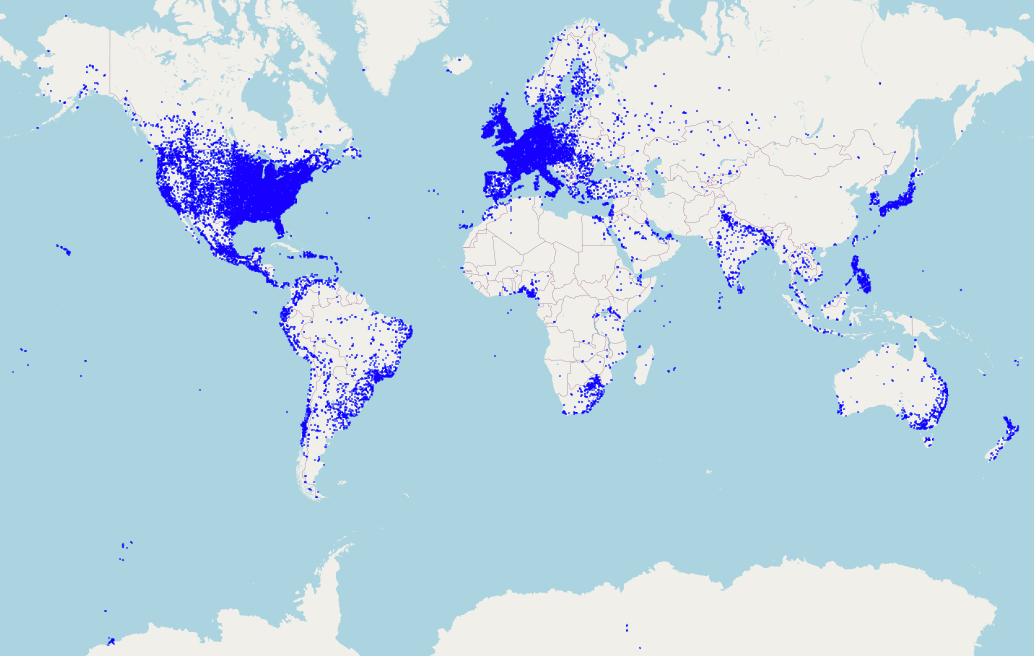Figure 1. Global distribution of AI citation locations mapped to H3 cells. Each point represents an H3 resolution-6 cell in which at least one AI citation was observed, illustrating the worldwide footprint of the 60,000+ locations scanned since July 2025.

Deep dive into the H3 geo-spatial system

H3 partitions the Earth's surface into hexagons arranged hierarchically. The grid is defined at sixteen resolutions. At resolution 0, the Earth is covered by hexagons with an area of roughly four million square kilometers. At resolution 15, the hexagons shrink to an area close to one square meter.

Each hexagon has a unique 64-bit identifier that encodes its resolution, its parent at the next coarser level, its children at the next finer level, its neighboring cells, and its polygon edge shapes. A hexagon at any resolution greater than zero references its parent one level up, and any hexagon at resolution fourteen or lower references its seven children whose centroids lie within its boundary. This hierarchical encoding makes aggregation and drill-down straightforward, and the included shape data allows any geospatial point or shape to be mapped into these cells. Figure 2 shows a cell with its associated child hexagons as well as the areas missed due to this imperfect mapping.

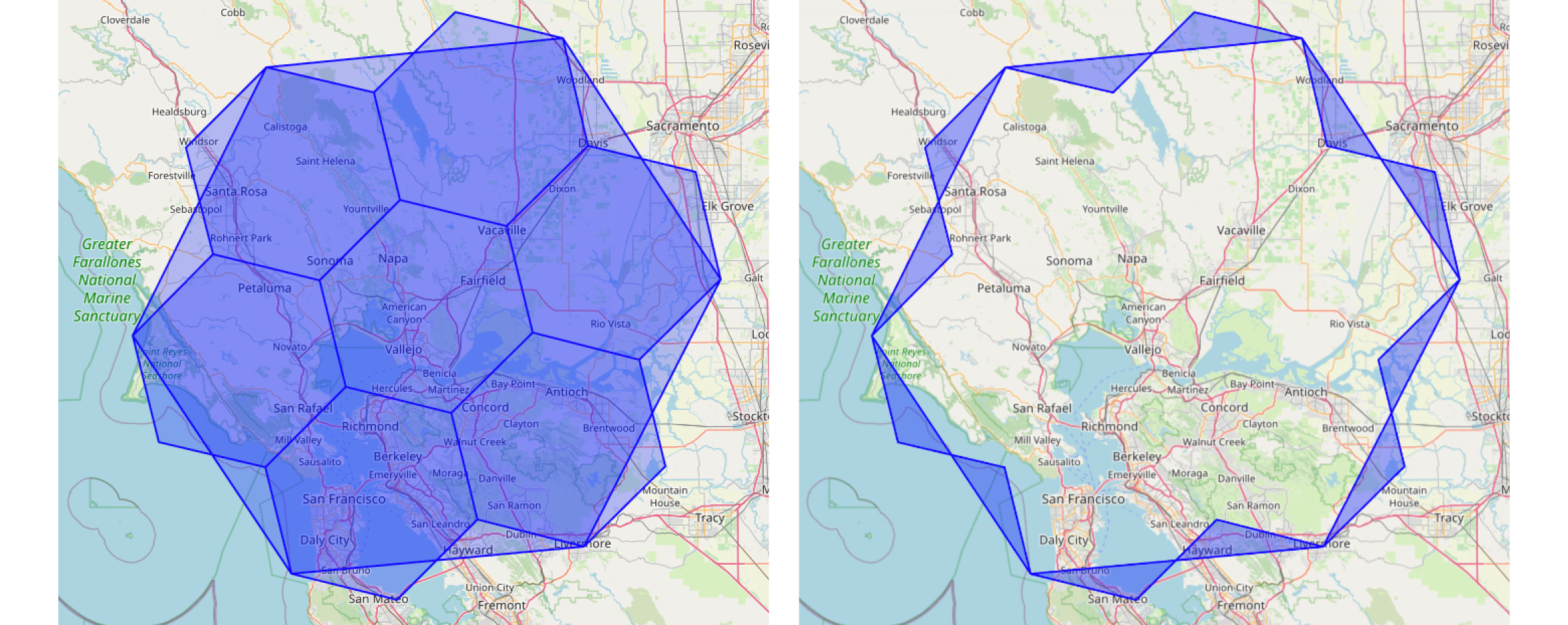
Figure 2. A hexagonal cell and its seven child cells with excluded areas.

Because the Earth is spherical, a perfect, congruent tiling with hexagons is impossible, so H3 incorporates a few pentagons that correct for spherical distortion. Locally, hexagons approximate planar tiling with high accuracy, and distortion decreases as resolution increases. The difference between the area of a parent hexagon and the sum of its seven children ranges from a neighborhood of about 0.2 percent at resolution 4 to a neighborhood of about 0.0001 percent at resolution 14. The centroids of children always fall within the parent, and if complete border coverage is required, polygons can be rasterized at higher resolutions so that all child cell centers lie within the parent's boundary.

Computational Properties

Hexagons are mathematically advantageous for spatial indexing. They approximate circles better than squares, and their six neighbors are equidistant from the center, which simplifies neighborhood operations. This is important for modeling diffusion, clustering, or movement. Unlike triangular tiling, which requires handling unequal edge relationships, hexagonal tiling provides uniform adjacency. In H3, spatial queries can be reduced to integer operations on 64-bit identifiers. Given only a latitude--longitude pair, the H3 library can compute the identifier of the containing hexagon, and from that identifier, all neighbor and hierarchy relationships can be derived. Since the identifiers are integers, they are efficient to store and fast to query, which makes H3 well-suited for large-scale indexing and retrieval.

Advantages Over ZIP Codes

The fundamental advantage of H3 over ZIP codes is that it is a globally consistent framework. It covers land, sea, and uninhabited regions with a single grid, eliminating the need for country-specific systems. Every cell at a given resolution is roughly equal in size and shape, thereby avoiding the sampling bias that arises from irregular administrative boundaries. The hierarchical nature of the grid enables the same analysis to be run at multiple scales without requiring changes to the underlying indexing method. A cell in New York City and a cell in rural Montana are structurally equivalent, and their relative influence is determined only by the data mapped to them rather than by arbitrary differences in boundary definitions.

ZIP codes are convenient identifiers but are less suitable as spatial indices because they are irregular, unstable, and geographically limited. H3 provides a globally standardized alternative. By partitioning the Earth into a hierarchical hexagonal grid, H3 enables consistent and efficient analysis of geospatial data at any scale. For systems such as the Scout Index, which require unbiased global coverage, H3 is not merely a substitute for ZIP codes but a universal indexing standard.

Taking the Scout Index global

Kontur.io provides a ready-to-use H3 global population density dataset at three resolutions, which we used to select cell centroids for assigning geo-location to our Scout Index.

We selected 3,000 locations, of which 1,000 were the most densely populated cells in the U.S.  For the other 2,000, we weighted each E.U. member country, the United Kingdom, and Australia by the square root of their total population to achieve a compromise between location diversity and fair representation.

When the sample size from each country is weighted by population, less populous countries like Denmark receive only a few cells. In contrast, countries like France and Germany are overrepresented in locations deemed lower-impact than a metroplex like Copenhagen. Figure 3 shows Denmark with and without square-root weighting at resolution 6.

A primary motivator of the Scout Index is to evaluate search performance and signals across a large population; therefore, this provides us with an appropriate balance.

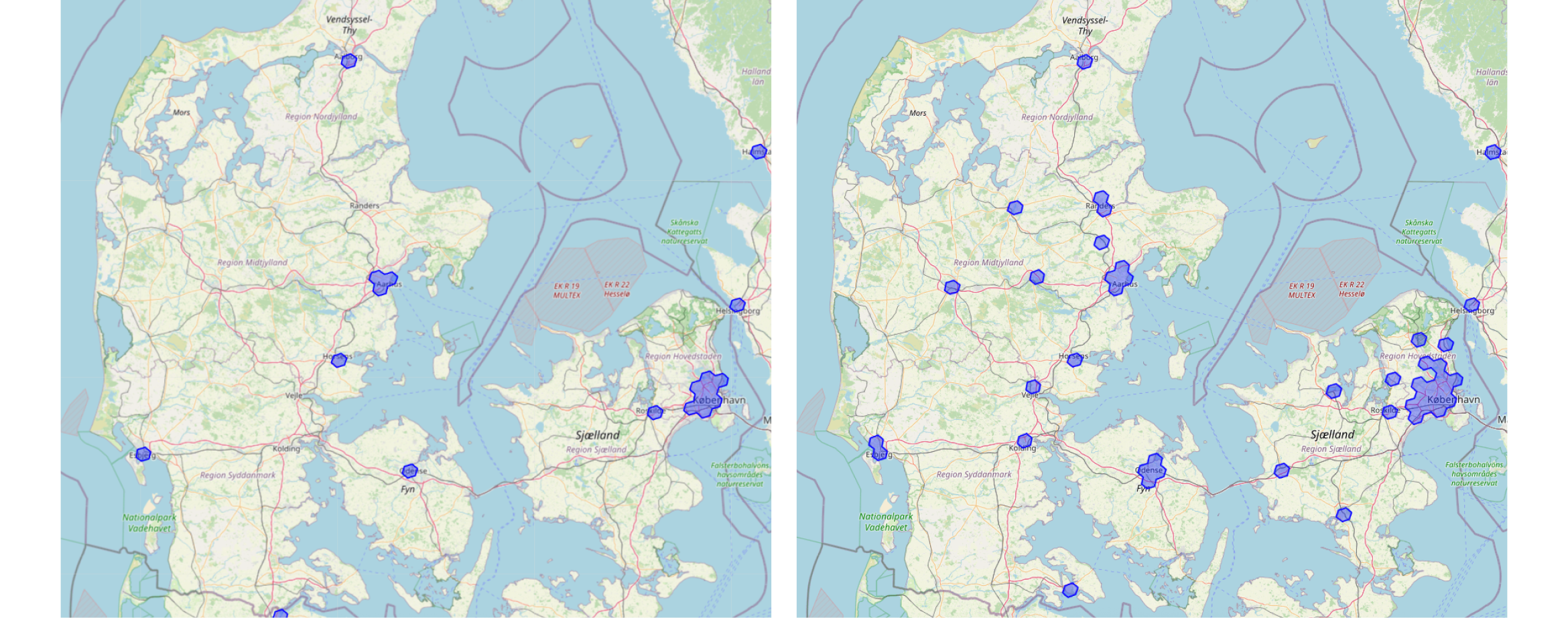Figure 3. Denmark without square root weighting (left) vs Denmark with square root weighting (right).

Selecting the right resolution

We evaluated the effect of H3 resolution on local business ranking behavior in Scout by varying the hexagon resolution used for search queries. To determine an appropriate resolution for analyses of local business performance, we selected 100 global locations and conducted experimental searches from the centroid of each hexagon at resolutions 4-9.

For comparison, we also ran a baseline search at each business' rooftop location. The results show that resolution six is the lowest resolution at which rank distributions diverge statistically from the rooftop baseline. Specifically, businesses were more likely to appear in the top 5 Google results when the query originated from the rooftop than from the centroid of the surrounding hexagons at resolution six. 

At this resolution, the edge length of a hexagon is approximately 3.2 km, corresponding to the maximum possible distance between the centroid and any point within the cell. This radius is broadly consistent with plausible travel ranges by foot, bicycle, or car in many urban and suburban areas. 

H3 resolution 6 strikes a practical balance between avoiding artificially inflated rankings by anchoring searches too closely to a business and modeling a realistic geography for local searches.

Challenges/Considerations

Choosing representative cells in the context of search patterns isn't straightforward because search behavior is tied to people, culture, and population density, not geography alone.  The H3 system provides uniform area coverage, but "representativeness" depends on many factors that may not be captured neatly by a hexagonal grid.

The search patterns of the population contained within a hexagon in a rural area of Montana are likely to be very different from the search patterns of a population from a hexagon in the heart of New York City.  Additionally, search patterns and SEO trends vary across the United States' different socio-geographical areas, and this will likely be the case in other countries as well.

In the future, we may allocate some portion of the Scout Index scan locations to lower-population areas by tuning a query parameter to sample from the first and second quartiles of the population-density-ranked H3 cells. For our most recent scan, only the most densely populated cells were chosen, all of which came from the top quartile.

Conclusion

The transition from ZIP codes to a hexagonal spatial index adopts a globally consistent geospatial framework, enabling large-scale SERP and AI analysis.  While ZIP codes have served as a practical unit for U.S.-based applications in the past, their irregular shapes, changing boundaries, and lack of international analogues make them ill-suited for global indexing.  In contrast, the H3 library provides a hierarchical, near-uniform tiling system that can be applied consistently worldwide.  This enables the seamless integration of disparate geospatial datasets and facilitates reproducibility and scalability.